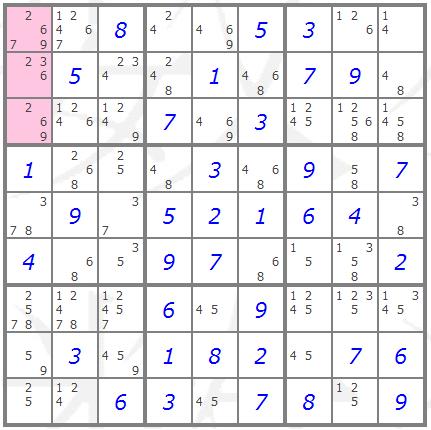
Pointing Pair

The pointing pair solving technique is an intermediate level solving technique. The objective of this solving method is to reduce the candidate lists of empty cells often revealing naked or hidden singles. There are two variations of this solving technique which allow candidates to be removed from the row or column or alternatively from the box.

Variation 1: Reducing row or column candidates
If a pair of empty cells within a box in the same row or column share a given candidate then that candidate can be removed from the candidate list of all other cells in the row or column if it is not a candidate of any of the other cells in the box.

The highlighted cells in the example below are a pointing pair. The candidate "7" of the highlighted cells is not a candidate of any of the other cells in the box containing the highlighted cells. This means that the "7" must be in one of the highlighted cells and can be removed from the candidate lists of any of the other cells in the row.



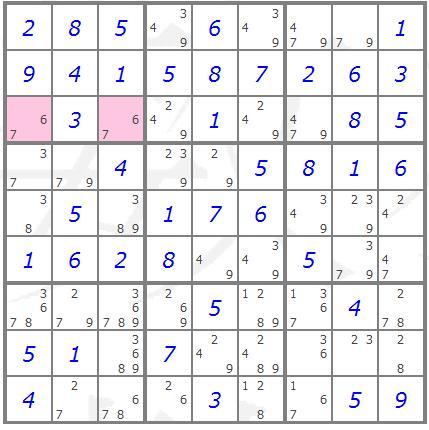
Variation 2: Reducing box candidates
If a pair of empty cells within a box in the same row or column share a given candidate, then that candidate can be removed from the candidate list of all other cells in the box if it is not a candidate of any other cells in the row or column.

The highlighted cells in the example below are a pointing pair. The candidate "7" of the highlighted cells is not a candidate of any of the other cells in the row to which the highlighted cells are "pointing". This means that the "7" must be in one of the highlighted cells and can be removed from the candidate lists of any of the other cells in the box.

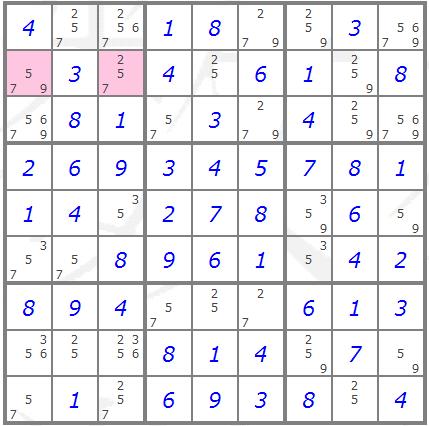
Pointing Triple

The pointing triple solving technique is simply an extension of the pointing pair solving technique to three cells. Please read the description of the pointing pair technique above before looking at the example below.

The highlighted cells in the example below are a pointing triple. The candidate "6" of the highlighted cells is not a candidate of any of the other cells in the column to which the highlighted cells are "pointing". This means that the "6" must be in one of the highlighted cells and can be removed from the candidate lists of any of the other cells in the box.